Преобразования потока управления
Преобразования потока управления изменяют граф потока управления одной функции. Они могут приводить к созданию в программе новых функций. Краткая характеристика методов приведена ниже.
Открытая вставка функций (function inlining) [5], п. 6.3.1 заключается в том, что тело функции подставляется в точку вызова функции. Данное преобразование является стандартным для оптимизирующих компиляторов. Это преобразование одностороннее, то есть по преобразованной программе автоматически восстановить вставленные функции невозможно. В рамках данной статьи мы не будем рассматривать подробно прямую вставку функций и её эффект на запутывание и распутывание программ.
Вынос группы операторов (function outlining) [5], п. 6.3.1. Данное преобразование является обратным к предыдущему и хорошо дополняет его. Некоторая группа операторов исходной программы выделяется в отдельную функцию. При необходимости создаются формальные параметры. Преобразование может быть легко обращено компилятором, который (как было сказано выше) может подставлять тела функций в точки их вызова.
Отметим, что выделение операторов в отдельную функцию является сложным для запутывателя преобразованием. Запутыватель должен провести глубокий анализ графа потока управления и потока данных с учётом указателей, чтобы быть уверенным, что преобразование не нарушит работу программы.
Непрозрачные предикаты (opaque predicates) [5], п. 6.1. Основной проблемой при проектировании запутывающих преобразований графа потока управления является то, как сделать их не только дешёвыми, но и устойчивыми. Для обеспечения устойчивости многие преобразования основываются на введении непрозрачных переменных и предикатов. Сила таких преобразований зависит от сложности анализа непрозрачных предикатов и переменных.
Переменная v является непрозрачной, если существует свойство

Непрозрачные предикаты могут быть трёх видов: PF - предикат, который всегда имеет значение "ложь", PT - предикат, который всегда имеет значение "истина", и P? - предикат, который может принимать оба значения, и в момент запутывания текущее значение предиката известно.
В работах [3], [7], [23] разработаны методы построения непрозрачных предикатов и переменных, основанные на "встраивании" в программу вычислительно сложных задач, например, задачи 3-выполнимости . Некоторые возможные способы введения непрозрачных предикатов и непрозрачных выражений вкратце перечислены ниже.
Использование разных способов доступа к элементы массива [23]. Например, в программе может быть создан массив (скажем, a), который инициализируется заранее известными значениями, далее в программу добавляются несколько переменных (скажем, i}, j), в которых хранятся индексы элементов этого массива. Теперь непрозрачные предикаты могут иметь вид a[i] == a[j]. Если к тому же переменные i} и j в программе изменяются, существующие сейчас методы статического анализа алиасов позволят только определить, что и i, и j могут указывать на любой элемент массива a.
Использование указателей на специально создаваемые динамические структуры [7]. В этом подходе в программу добавляются операции по созданию ссылочных структур данных (списков, деревьев), и добавляются операции над указателями на эти структуры, подобранные таким образом, чтобы сохранялись некоторые инварианты, которые и используются как непрозрачные предикаты.
Конструирование булевских выражений специального вида [3].
Построение сложных булевских выражений с помощью эквивалентных преобразований из формулы true. В простейшем случае мы можем взять k произвольных булевских переменных x1...xk и построить из них тождество
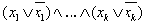
Использование комбинаторных тождеств, например
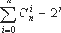
Внесение недостижимого кода (adding unreachable code). Если в программу внесены непрозрачные предикаты видов PF или PT, ветки условия, соответствующие условию "истина" в первом случае и условию "ложь" во втором случае, никогда не будут выполняться. Фрагмент программы, который никогда не выполняется, называется недостижимым кодом. Эти ветки могут быть заполнены произвольными вычислениями, которые могут быть похожи на действительно выполняемый код, например, собраны из фрагментов той же самой функции. Поскольку недостижимый код никогда не выполняется, данное преобразование влияет только на размер запутанной программы, но не на скорость её выполнения. Общая задача обнаружения недостижимого кода, как известно, алгоритмически неразрешима. Это значит, что для выявления недостижимого кода должны применяться различные эвристические методы, например, основанные на статистическом анализе программы.
Внесение мёртвого кода (adding dead code) [5], п. 6.2.1. В отличие от недостижимого кода, мёртвый код в программе выполняется, но его выполнение никак не влияет на результат работы программы. При внесении мёртвого кода запутыватель должен быть уверен, что вставляемый фрагмент не может влиять на код, который вычисляет значение функции. Это практически значит, что мёртвый код не может иметь побочного эффекта, даже в виде модификации глобальных переменных, не может изменять окружение работающей программы, не может выполнять никаких операций, которые могут вызвать исключение в работе программы.
Внесение избыточного кода (adding redundant code) [5], п. 6.2.6. Избыточный код, в отличие от мёртвого кода выполняется, и результат его выполнения используется в дальнейшем в программе, но такой код можно упростить или совсем удалить, так как вычисляется либо константное значение, либо значение, уже вычисленное ранее. Для внесения избыточного кода можно использовать алгебраические преобразования выражений исходной программы или введение в программу математических тождеств.
Например, можно воспользоваться комбинаторным тождеством
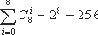
Подобные алгебраические преобразования ограничены целыми значениями, так как при выполнении операций с плавающей точкой возникает проблема накопления ошибки вычислений. Например, выражение sin2x+cso2x при вычислении на машине практически никогда не даст в результате значение 1. С другой стороны, при операциях с целыми значениями возникает проблема переполнения. Например, если использование 32-битной целой переменной x заменено на выражение x * p / q, где p и q гарантированно имеют одно и то же значение, при выполнении умножения x * p может произойти переполнение разрядной сетки, и после деления на q получится результат не равный p. В качестве частичного решения задачи можно выполнять умножение в 64-битных целых числах.
Преобразование сводимого графа потока управления к несводимому (transforming reducible to non-reducible flow graph) [5], п. 6.2.3. Когда целевой язык (байт-код или машинный язык) более выразителен, чем исходный, можно использовать преобразования, "противоречащие" структуре исходного языка. В результате таких преобразований получаются последовательности инструкций целевого языка, не соответствующие ни одной из конструкций исходного языка.
Например, байт-код виртуальной машины Java содержит инструкцию goto, в то время как в языке Java оператор goto отсутствует. Графы потока управления программ на языке Java оказываются всегда сводимыми, в то время как в байт-коде могут быть представлены и несводимые графы.
Можно предложить запутывающее преобразование, которое трансформирует сводимые графы потока управления функций в байт-коде, получаемых в результате компиляции Java-программ, в несводимые графы. Например, такое преобразование может заключаться в трансформации структурного цикла в цикл с множественными заголовками с использованием непрозрачных предикатов.
С одной стороны, декомпилятор может попытаться выполнить обратное преобразование, устраняя несводимые области в графе, дублируя вершины или вводя новые булевские переменные. С другой строны, распутыватель может с помощью статических или статистических методов анализа определить значение непрозрачных предикатов, использованных при запутывании, и устранить никогда не выполняющиеся переходы. Однако, если догадка о значении предиката окажется неверна, в результате получится неправильная программа.
Устранение библиотечных вызовов (eliminating library calls) [5], п. 6.2.4. Большинство программ на языке Java существенно используют стандартные библиотеки. Поскольку семантика библиотечных функций хорошо известна, такие вызовы могут дать полезную информацию при обратной инженерии программ. Проблема усугубляется ещё и тем, что ссылки на классы библиотеки Java всегда являются именами, и эти имена не могут быть искажены.
Во многих случаях можно обойти это обстоятельство, просто используя в программе собственные версии стандартных библиотек. Такое преобразование не изменит существенно время выполнения программы, зато значительно увеличит её размер и может сделать её непереносимой.
Для программ на традиционных языках эта проблема стоит менее остро, так как стандартные библиотеки, как правило, могут быть скомпонованы статически вместе с самой программой. В данном случае программа не содержит никаких имён функций из стандартной библиотеки.
Переплетение функции (function interleaving) [5], п. 6.3.2. Идея этого запутывающего преобразования в том, что две или более функций объединяются в одну функцию. Списки параметров исходных функций объединяются, и к ним добавляется ещё один параметр, который позволяет определить, какая функция в действительности выполняется.
Клонирование функций (function cloning) [5], п. 6.3.3. При обратной инженерии функций в первую очередь изучается сигнатура функции, а также то, как эта функция используется, в каких местах программы, с какими параметрами и в каком окружении вызывается.
Анализ контекста использования функции можно затруднить, если каждый вызов некоторой функции будет выглядеть как вызов какой-то другой, каждый раз новой функции. Может быть создано несколько клонов функции, и к каждому из клонов будет применён разный набор запутывающих преобразований.
Развёртка циклов (loop unrolling) [5], п. 6.3.4. Развёртка циклов применяется в оптимизирующих компиляторах для ускорения работы циклов или их распараллеливания. Развёрка циклов заключается в том, что тело цикла размножается два или более раз, условие выхода из цикла и оператор приращения счётчика соответствующим образом модифицируются. Если количество повторений цикла известно в момент компиляции, цикл может быть развёрнут полностью.
Разложение циклов (loop fission) [5], п. 6.3.4. Разложение циклов состоит в том, что цикл с сложным телом разбивается на несколько отдельных циклов с простыми телами и с тем же пространством итерирования.
Реструктуризация графа потока управления [24]. Структура графа потока управления, наличие в графе потока управления характерных шаблонов для циклов, условных операторов и т. д. даёт ценную информацию при анализе программы. Например, по повторяющимся конструкциям графа потока управления можно легко установить, что над функцией было выполнено преобразование развёртки циклов, а далее можно запустить специальные инструменты, которые проанализируют развёрнутые итерации цикла для выделения индуктивных переменных и свёртки цикла. В качестве меры противодействия может быть применено такое преобразование графа потока управления, которое приводит граф к однородному ("плоскому") виду. Операторы передачи управления на следующие за ними базовые блоки, расположенные на концах базовых блоков, заменяются на операторы передачи управления на специально созданный базовый блок диспетчера, который по предыдущему базовому блоку и управляющим переменным вычисляет следующий блок и передаёт на него управление. Технически это может быть сделано перенумерованием всех базовых блоков и введением новой переменной, например state, которая содержит номер текущего исполняемого базового блока.
Запутанная функция вместо операторов if, for и т. д. будет содержать оператор switch, расположенный внутри бесконечного цикла.
Локализация переменных в базовом блоке [3]. Это преобразование локализует использование переменных одним базовым блоком. Для каждого запутываемого базового блока функции создаётся свой набор переменных. Все использования локальных и глобальных переменных в исходном базовом блоке заменяются на использование соответствующих новых переменных. Чтобы обеспечить правильную работу программы между базовыми блоками вставляются так называемые связующие (connective) базовые блоки, задача которых скопировать выходные переменные предыдущего базового блока в входные переменные следующего базового блока.
Применение такого запутывающего преобразование приводит к появлению в функции большого числа новых переменных, которые, однако, используются только в одном-двух базовых блоках, что запутывает человека, анализирующего программу.
При реализации этого запутывающего преобразования возникает необходимость точного анализа указателей и контекстно-зависимого межпроцедурного анализа. В противном случае нельзя гарантировать, что запись по какому-либо указателю или вызов функции не модифицируют настоящую переменную, а не текущую рабочую копию.
Расширение области действия переменных [5], п. 7.1.2. Данное преобразование по смыслу обратно предыдущему. Это преобразование пытается увеличить время жизни переменных настолько, насколько можно. Например, вынося блочную переменную на уровень функции или вынося локальную переменную на статический уровень, расширяется область действия переменной и усложняется анализ программы. Здесь используется то, что глобальные методы анализа (то есть, методы, работающие над одной функцией в целом) хорошо обрабатывают локальные переменные, но для работы со статическими переменными требуются более сложные методы межпроцедурного анализа.
Для дальнейшего запутывания можно объединить несколько таких статических переменных в одну переменную, если точно известно, что переменные не могут использоваться одновременно.Очевидно, что преобразование может применяться только к функциям, которые никогда не вызывают друг друга непосредственно или через цепочку других вызовов.
